円とおうぎ形の「ツボ」(中1)
基本1 円
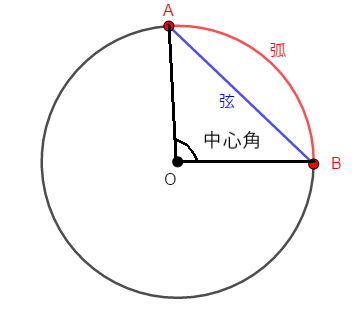
円の弧と弦
円の円周上に2点A、Bをとるとき、図のAからBまでの部分を、「弧」といい、弧ABと表すよ。
また、弧ABの両端を結んだ線分のことを、「弦」といい、弦ABと表すよ。
円の中心Oと円周上の2点A、Bを結んでできた∠AOBを弧ABに対する「中心角」というよ。

曲線の部分を弧と呼ぶ身近な例としては、括弧(かっこ)の弧があるね。
円と直線
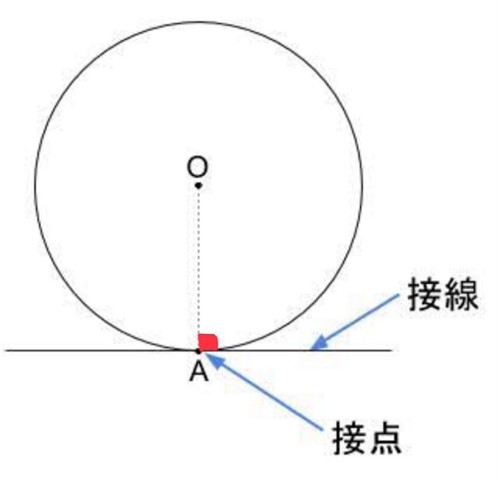
円と直線が1点だけを共有するとき、直線は円に接するという。
また、左の図のように、直線が円Oに接している時、その直線を円Oの「接線」といい、接する点Aを「接点」という。
車は地面を走っているけど、タイヤは円だから、タイヤにとって地面は接線にあたるよ。
円の接線は、その接点を通る半径に必ず垂直になるよ!!

もし接線である地面に対して円形のタイヤが垂直に接していなければ、車はまっすぐ走れなくなってしまうよね!!

基本2 おうぎ形
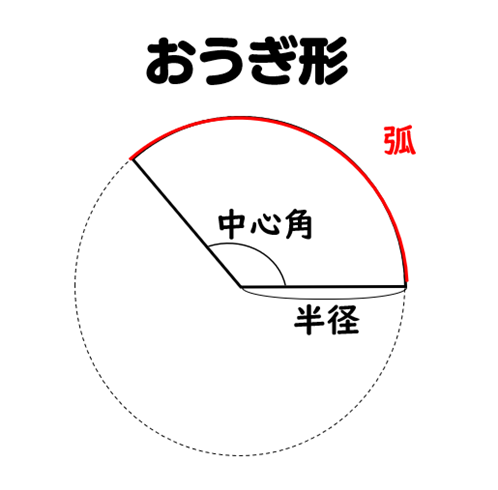
おうぎ形とは
円の2つの半径と弧で囲まれた図形を、おうぎ形といいます。
また、おうぎ形の2つの半径がつくる角を、そのおうぎ形の中心角というよ。

おうぎとは、右のように中心角を変えられる扇子のことだよ。
おうぎ形の性質
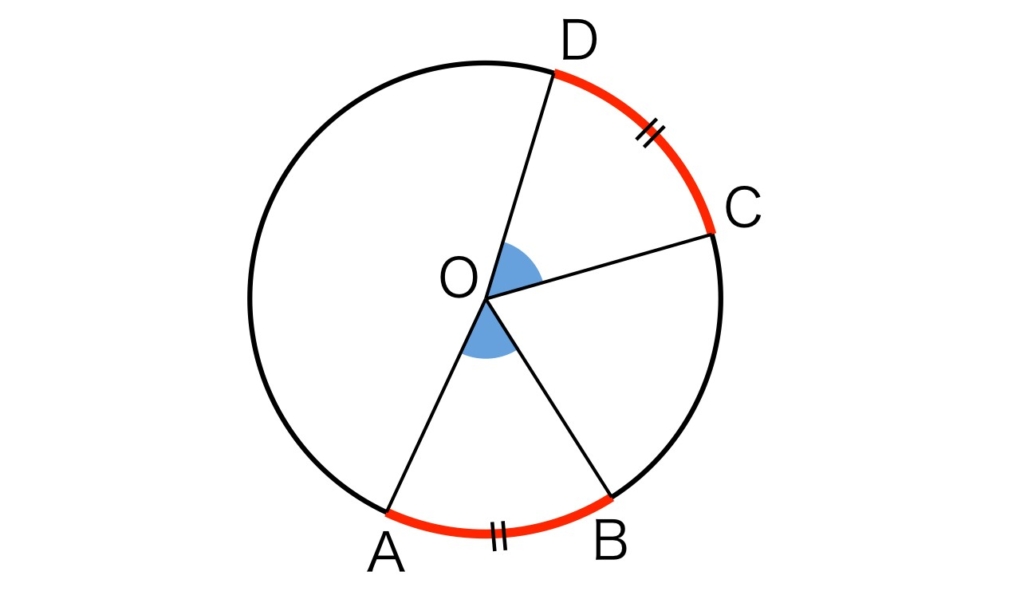
おうぎ形は、円の2つの半径と弧で囲まれた図形だから、左の図のように、それぞれのおうぎ形の半径と中心角が等しい場合、合同になり、弧の長さや面積もそれぞれ等しくなるよ。
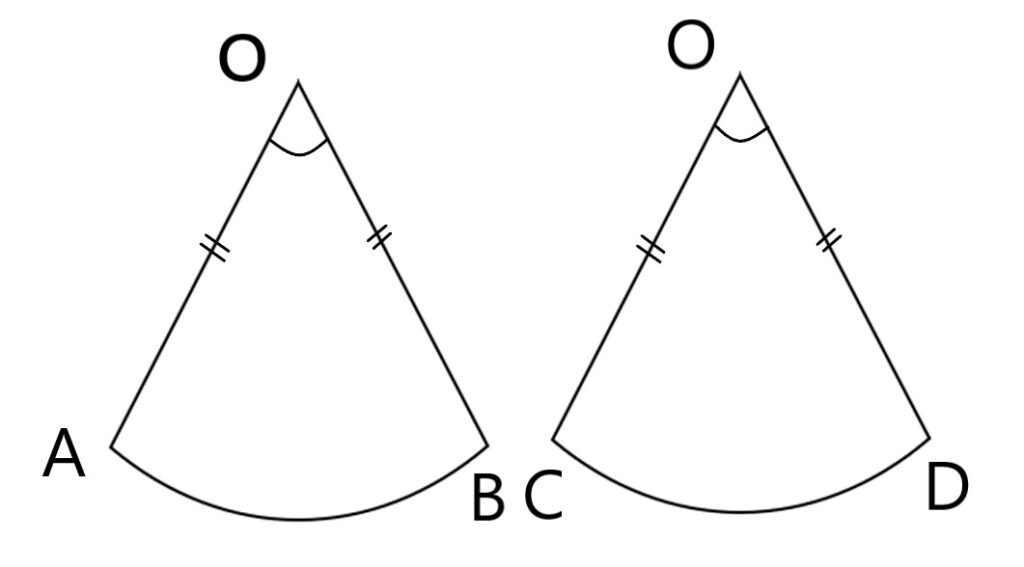
2つのおうぎ形を取り出して比べると、弧の長さも面積も等しいことがわかるね。
基本3 円の周の長さと面積
円周率
円の周りのことを円周と言いますが、その長さを求めるために、小学校では、円周=直径×3.14という式で計算をしてきました。そして、この3.14で表されていた数字のことを円周率といいます。
例えば、直径14cmの円周の長さは、 14×3.14=43.96(cm) と求めていましたね。
円周率がどんな数字であるのかは、古代から研究されてきました、一番最初は、実際に円を描き、円周の長さを測った上で、直径で割って求めていたようです。円はどんな大きさでも、形は同じなので、(これを相似と言うよ。)円周÷直径の値は常に一定になるはずです。そこで、以下のように検証がされていました。
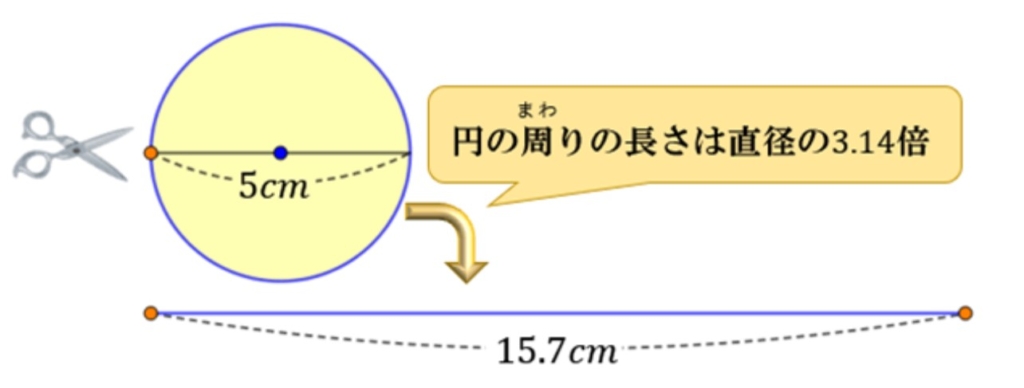
直径5㎝の円の周りに、ひもを巻きつけ、その長さを測ると、15.7cmになりました。
15.7cm÷5=3.14
円の周りの長さは、直径の約3.14倍とわかりました。
その後、円周率をもっと正確に求めたいと研究が進んだ結果、アルキメデスの原理で有名なアルキメデスが円周率は、「3.14084…<円周率<3.14285…」ということまで証明しました。
このように求められた円周率ですが、中学生からはギリシア文字のπ(パイ)で表します。

円周率を表すのにπが使われている理由は、
「円周、周辺、周り」などを意味するギリシア語
「ペリフェレイア」(περιφερεια)の頭文字に由来するよ。
円の周の長さと面積
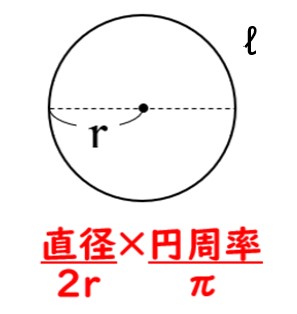
円の周の長さを求める時、小学校までは、直径×3.14で計算していましたが、中学校になると、左の図のように直径は半径を2倍したものと考え、円周率もπを使います。
したがって、円周の長さをℓとすると
周の長さは ℓ=2πr で求められます。
(例) 半径7cmの円周の長さは、 2π×7=14π(cm)
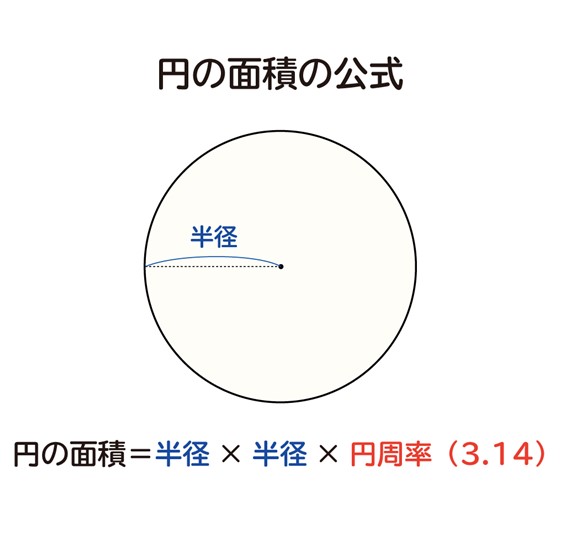
一方、円の面積を求める時、小学校では右の公式にあてはめて求めていました。
例えば、半径7cmの円の面積は
7×7×3.14=153.86㎠となります。
一方、中学では、円周率をπと表しますので
円の面積=πr²で求めることになります。
よって、上の例では、49π(㎠)となります。
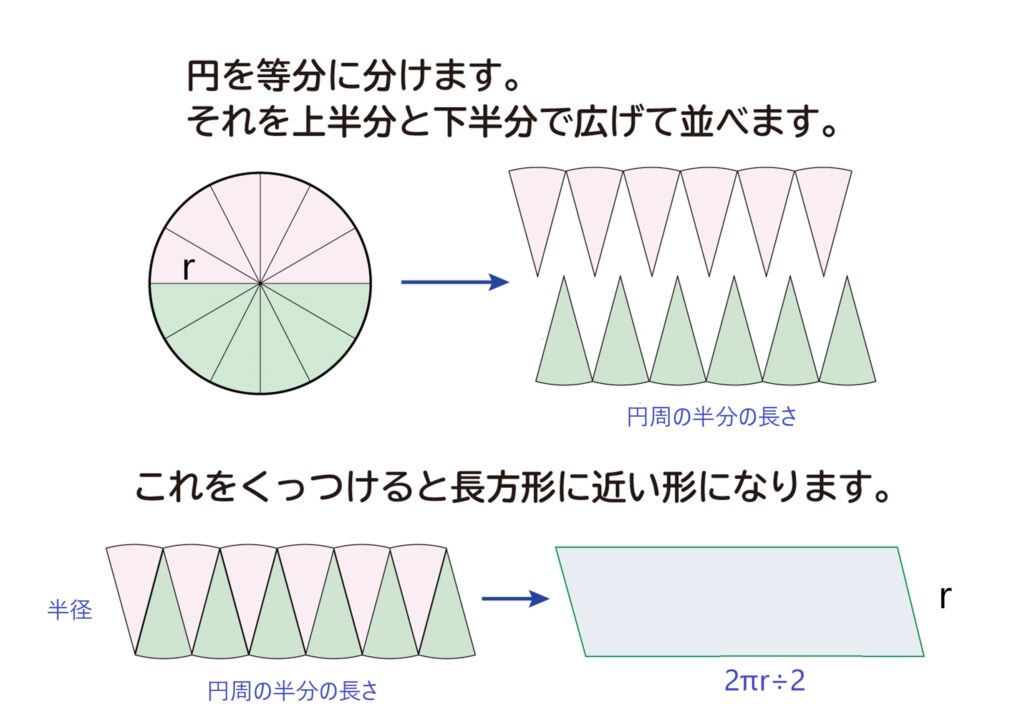
ここで、円の面積の求め方を復習しておこう‼

左の図のように円を等分に分けて並べ替えると長方形に近い形になります。
たてが半径r。横は円周の半分の長さだから$2πr÷2$。$r×2πr÷2=πr²$となるから、
円の面積$=πr²$が導かれるんだったね。
基本4 おうぎ形の弧の長さと面積
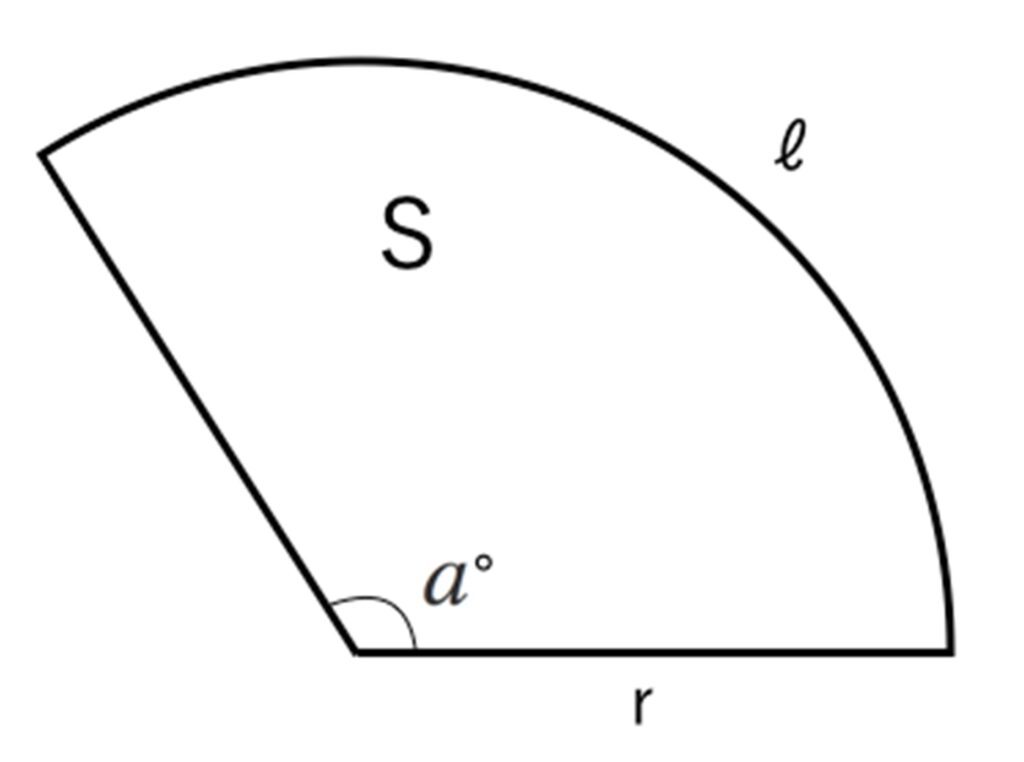
半径r、中心角a°のおうぎ形の弧の長さをℓ、面積をSとすると、
弧の長さ ℓ=$2πr× \frac{a}{360} $
面積 S=$πr²× \frac{a}{360} $
ディスカッション
コメント一覧
まだ、コメントがありません